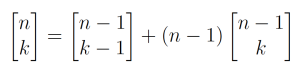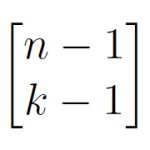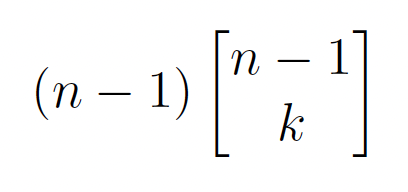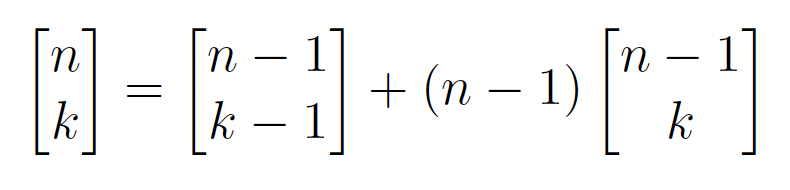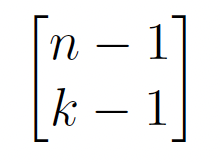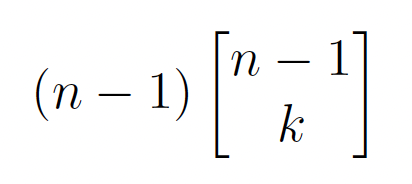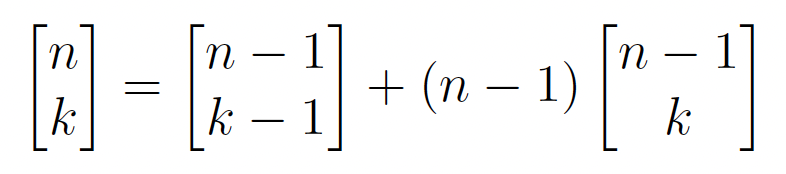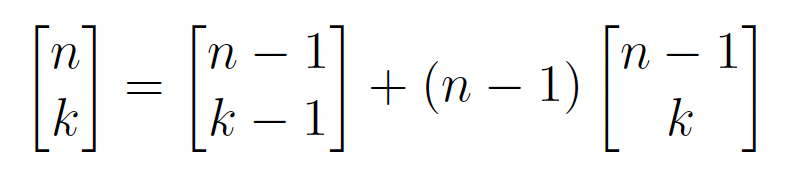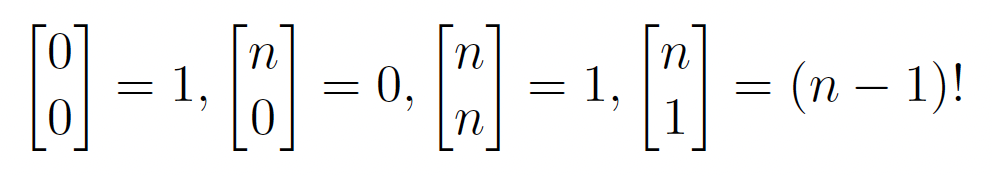Permutations of [n] with k Cycles and Left-to-Right Maxima
by Blake Voyles, Mathematics
Background
What is a permutation?
A permutation is an ordered arrangement of elements. More specifically, a permutation of n is a unique arrangement of the set {1, 2, 3, …, (n − 1), n}. For example, the permutations of 3 are the following:
{1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}
The total amount of permutations of [n] is always n!. Similarly, permutations of [n − 1] are always n!, and the same is true for sets starting at 2 ({2, 3, 4, …, n}).
What is a cycle?
A cycle is a subset of permutations with all elements in the subset trading positions. A permutation cycle is cyclic meaning that the last element of the cycle goes to the first element of the cycle. Cycle notation is a way to write a permutation that breaks down the elements into their cycles. There are also three ways to write permutations in cycle notation: two line, one line, and cycle notation. For the purposes of this paper, only one line and cycle notation will be used. For example, the cycle notations of {2, 1, 3} (a specific permutation of 3) are the following:
One Line: (2, 1, 3) Cycle Notation: (12)(3)
The elements 1,2 trade positions in the permutation, and the 3 is in its own cycle because it stays in the same position.
What are left-to-right maxima in a permutation?
Given an element in a permutation of numbers (1 to n), it is a left-to-right maxima when the given element is greater than all the other elements to the left of the given element. For example, given the permutation (1, 3, 2, 5, 4) of 5. There are exactly 3 left- to-right maxima, those being 1,3, and 5. The first element of a permutation will always be a left-to-right maxima.
What does it mean for a permutation of [n] to have exactly k cycles?
Every permutation of [n] can be written as a sequence of cycles. The cycle of a permutation is a subset of the permutation where the elements are moved to the position of the next element in the cycle. A permutation cycle is cyclic meaning that the last element of the cycle goes to the first element of the cycle. A permutation of [n] with k cycles is a permutation that has exactly k of the subset cycles, including cycles that are a single element (which are said to be mapped to themselves).
Claim
Let f : [n] → [n] be a permutation of [n]. The number of permutations of [n] with k left-to-right maxima is equal to the number of permutations of [n] with exactly k cycles (including fixed points). To prove this claim, we will show that the amount of both sets of permutations follows the recursive formula for the unsigned Stirling numbers of the first kind and that the two sets start with equivalent base cases.
For example, let n = 3 and k = 2:
Permutations with 2 cycles: (1)(32), (13)(2), (12)(3)
Permutations with 2 left-to-right maxima: {1, 3, 2}, {2, 1, 3}, {2, 3, 1}
Unsigned Stirling Numbers of the First Kind
It is well known that the unsigned Stirling numbers of the first kind are the number of permutations of [n] with k cycles, but we will still break down how the recursive formula is found from the cycles. The recursive formula for the unsigned Stirling numbers of the first kind is only made up of two terms and they are as follows (formula 1.0):
Recursion for Permutations of [n] with Exactly k Cycles
As mentioned earlier the recursive formula for the unsigned Stirling numbers of the first kind gives you the number of per- mutations of [n] with exactly k cycles. To start we need to establish the trivial cases or the base cases. The true base case is that any permutation of 0 with 0 cycles is 1. The rest is assuming the initial condition that n > 0. Any permutation of [n] into 0 cycles is 0, because there is no permutation with n > 1 with no cycles. The third trivial case is that the number of permutations of [n] with n cycles is only 1 because this would be the permutation where every cycle is of length 1. This gives n cycles of length one, in other words, every element is a fixed point. The final trivial case is the number of permutations of [n] with 1 cycle is equivalent to (n − 1)!, and this is because a permutation of n with 1 cycle is equivalent to fixing the first value and permuting the (n − 1) elements. The total amount of possibilities for a permutation of length n is n!, so with the first element fixed the rest of the permutation is equal to (n − 1).
When trying to form all the permutations of [n] with k cycles, there are two options. The new element can be added as a new cycle, or it can be added into an existing cycle. To show how the permutations of [n] with k cycles follows formula 1.0, we will go through the reasoning for the first and then the second term. The first term in 1.0 counts all the permutations where the new term is added as a single cycle. If we are trying to get permutations of [n] with k cycles, we can add a cycle of length 1 to all the permutations of (n – 1) with (k – 1) cycles. The additional cycle of length 1 would be the nth term as a fixed point. The new permutations are now all permutations of [n] with (k – 1) + 1 cycles, or better put permutations of [n] with k cycles. For example, let’s say that we want a permutation of 4 with 2 cycles. Consider the following permutation of 3: (2, 3, 1). This is a permutation of (4 − 1) with exactly (2 − 1) cycles. To get the target permutation of 4 with 2 cycles, it is easy to add a single cycle (4) to the end. The new permutation is now (2, 3, 1, 4), which is a permutation of 4 with exactly 2 cycles those being (1, 3, 2)(4).
This gives us the first part formula 1.0, which would be
The second term in 1.0 counts all the permutations where the new term is added to an existing cycle. To do this and still end with a permutation of n with k cycles, we have to start with a permutation of (n – 1) with k cycles. This is because when adding the new term anywhere we are increasing the permuta- tion from one of (n – 1) to a permutation of n. The reason we are starting with k cycles this time is because we aren’t adding the nth element as a new cycle, so the total number of cycles before the nth is added stays the same. The new term can be added anywhere within the permutation, and there are (n – 1) options for where to place the new term. For example, let’s say that we want another permutation of 4 with 2 cycles. Consider the following permutation of 3: (1, 3, 2). In this permutation, there are already two cycles, (1), (2, 3). We can add the 4 after the 1, 3, or 2. That is a total of (4 − 1) options, and say we add the 4 after the 3. The permutation is now (1, 3, 4, 2), with the two cycles being (1)(2, 4, 3).
This gives us the second term of formula 1.0 which would be
Because the nth term can only be added as a new cycle of length 1 or into an existing cycle, these two terms account for all the permutations of [n] with k cycles. This means that the recursive formula for the number of permutations of [n] with k cycles is the following (1.0):
Recursion for permutations of [n] with k left-to-right maxima
Again, to start we need to establish the trivial cases or the base cases. The true base case is that any permutation of 0 with 0 left-to-right maxima is 1. The rest is assuming the initial condition that n > 0. The first trivial case is the amount of permutations of [n] with 0 left-to-right maxima is also 0. This is because the first element of every permutation is a left-to-right maxima. The second trivial case is the number of permuta- tions of [n] with n left-to-right maxima is only 1, and this is because the only possible way for every element to be a left-to- right maxima is when the permutation of n is just the elements in ascending order. If all elements are not in ascending order, then there will be at least one element that is not a left-to-right maxima. The last trivial case is the amount permutation of n with 1 left-to-right maxima is equivalent to (n − 1)!. Since the first element is always a left-to-right maxima, this is the case when the largest element is also the first element in the permutation. Because every element is less than the largest, the only left-to-right maxima would be the first element. The amount of permutations that this applies to is equivalent to (n − 1)! because the first term is fixed (having to be the largest element) and this leaves (n − 1) elements with the freedom to be placed in any order. This is essentially a permutation of (n − 1) which is exactly (n − 1)!.
When trying to form all the permutations of [n] with k left-to- right maxima, there are two categories of permutations. Those two categories are permutations of [n] with k left-to-right max- ima that start with a 1 or don’t start with a 1, and these two categories are represented by the first and second term in the recursive formula mentioned previously.
The first term counts all the permutations of [n] with k left- to-right maxima that start with a 1. Because of the rule that the first term is always a left-to-right maxima, the 1 being in the first term is significant. Other than permutations of just 1, the first element being 1 is the only way that 1 can be a left-to-right maxima. If we were trying to get permutations of [n] with k left- to-right maxima, we could start with a permutation of (n − 1). Instead of this permutation being the usual permutation containing the elements 1 to (n− 1), let’s say that the permutation contains elements from 2 to n. There are still a total of (n − 1) elements so all the properties hold for this newly shifted set of permutations. The first term counts all these shifted permuta- tions of 2 to (n – 1) with (k – 1) left-to-right maxima. To get the permutations of [n] with k left-to-right maxima we take the shifted permutations of (n – 1) with (k – 1) left-to-right maxima, and add a 1 to the beginning of the permutation. When this is done, the permutation is now the complete permutation of n, and because the first element is always a left-to-right maxima, adding the 1 increases the count of left-to-right-maxima from (k − 1) to k. This operation gives results in a permutation of n with k left-to-right maxima, which is exactly what we needed. For example, let’s say we want a permutation of 4 with 2 left-to- right maxima. Consider the following permutation of 3: (3, 1, 2). We then would add 1 to all the elements, resulting in the per- mutation (4, 2, 3). Then to complete the transformation add a 1 to the beginning of the permutation, giving us the permutation (1, 4, 2, 3). This is now a permutation of 4 with 2 left-to-right maxima, which was derived from a permutation of (4 − 1) with (2 − 1) left-to-right maxima.
This gives us the first part of the recursive formula, which would be
The second term counts all the permutations where the 1 is not the first element. When 1 is not the first element is always true that it is not a left-to-right maxima within a permutation. We will start by doing the same thing we did when explaining the first term. Instead of the normal permutation of (n – 1), we will use the permutation starting at 2 going to n. Again, this new set of permutations has all the same properties as the nor- mal set, but with every term shifted up 1. In order to add the 1, and still end with a permutation of n with k left-to-right max- ima we have to start with the shifted permutation of (n−1), but with k left-to-right maxima before adding the 1. This is exactly the amount of permutations of (n – 1) with k left-to-right max- ima. We now need to add the one into the permutation, with the only restriction being that it can’t go in front of the first el- ement. That leaves us with exactly (n− 1) possible positions to place the 1. This second term is the amount of possible positions (n− 1) multiplied by the amount of permutations of (n – 1 with k left-to-right maxima. For example, let’s say that we want a permutation of 4 with exactly 2 left-to-right maxima. Consider the following permutation of 3: (2, 3, 1). This permutation al- ready has 2 left-to-right maxima. We then again add 1 to all the elements of the permutation, resulting in the new permutation being (3, 4, 2). This permutation still only has 2 left-to-right- maxima. We can add the 1 after the 3, 4, or 2, and doing so will not increase the number of left-to-right maxima. Let’s add the 1 after the 3, which gives us the final permutation (3, 1, 4, 2). This is a permutation of 4 with 2 left-to-right maxima that was derived by a permutation of 3 with 2 left-to-right maxima. This gives us the following second term for the recursive formula for permutations of [n] with k left-to-right maxima:
Because all permutations fit into one of the two categories of starting with a 1 or not starting with a 1, the number of permu- tations of [n] with k left-to-right maxima can be counted using only these two terms. This means that the recursive formula for the number of permutations of [n] with k left-to-right maxima is the following (1.0):
Conclusion
We have justified the recursive formula for both the amount of permutations of [n] with k cycles and the amount of permutations of [n] with k left-to-right maxima. The two have the exact same recursive formula being (1.0),
This doesn’t necessarily mean that the two are equal. For the two to be equivalent, they must also have the same base cases. Both have the following trivial and base cases:
The number of permutations of [n] with exactly k cycles and the number of permutations of [n] with k left-to-right maxima have identical recursive formulas and have the exact same base cases, therefore the two are equivalent. They both start out the same because they have equivalent base cases. Any n and k when plugged into the recursive formula will undergo the same operations and will end with the same base cases, so when deter- mining the amounts for any given n and k for both the number of permutations of [n] with exactly k cycles and the number of permutations of [n] with k left-to-right maxima the resulting amounts are the same.